Experimentos con CircularString en Denali

Continúo revisando algunas de las mejoras que ofrece SQL Denali. En este caso el soporte para figuras circulares. Este post resume algunas conclusiones de experimentos con el nuevo CircularString. Antes de iniciar:

1. Limito el análisis al uso de CircularString con un solo segmento, en lugar de la colección que el tipo soporta.
2. SMS (SQL Server Management Studio) en CTP3 no dibuja segmentos circulares, por lo que cuando quiera visualizar los datos usare la función CurveToLineWithTolerance.
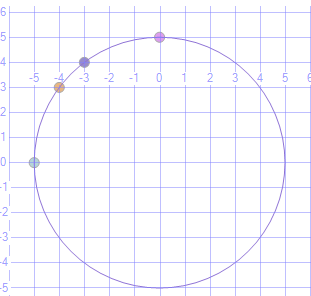
3. Para facilitar los cálculos usare un círculo base con centro (0, 0) y con radio 5. Este círculo se escoge porque es fácil también usar coordenadas con pares usando números enteros.

1) Declaración de CircularString

El CircularString de un solo segmento se construye usando tres puntos de un plano.

— Declaracion Valida sin Elevacion

DECLARE@g1geometry=geometry::STGeomFromText(‘CIRCULARSTRING(-5 0, -4 3, 0 5)’, 0);

— Declaracion Valida: Con la misma elevacion en todos los puntos

DECLARE@g2geometry=geometry::STGeomFromText(‘CIRCULARSTRING(-5 0 2, -4 3 2, 0 5 2)’, 0);

— Declaracion invalida: no todos los puntos tienen la misma elevacion

DECLARE@g3geometry=geometry::STGeomFromText(‘CIRCULARSTRING(-5 0 2, -4 3 1, 0 5 2)’, 0);

Las primeras dos declaraciones son válidas: la primera es la más común, la segunda permite usar la elevación (Z). La tercera declaración es invalida porque los puntos no están en la misma elevación, por lo que genera una excepción.

2) Conversión Implícita

Aunque no está directamente relacionado con el CircularString vale la pena mencionar que el tipo de datos geométrico soporta conversión implícita de texto. El siguiente código:

— Conversion Implicita

DECLARE@g1geometry=geometry::STGeomFromText(‘CIRCULARSTRING(-5 0, -4 3, 0 5)’, 0);

DECLARE@g2geometry=’CIRCULARSTRING(-5 0, -4 3, 0 5)’;– Conversion Implicita

SELECT@g1.STEquals(@g2), @g2.STEquals(@g1)

,@g1.ToString(), @g2.ToString();

Demuestra que la primera y segunda declaración son equivalentes. Como la segunda es más simple es lo que seguiré usando en el posteo.

1. Figuras Vacías

Un CircularString puede estar vacío y es igual a cualquier otra figura geométrica vacía.

— Curva Vacia

DECLARE@g1geometry=’CIRCULARSTRING EMPTY’;

DECLARE@g2geometry=’GEOMETRYCOLLECTION EMPTY’;        — Tambien:

— POINT, LINESTRING, POLYGON

— MULTIPOINT, MULTILINESTRING, MULTIPOLYGON

SELECT@g1.STEquals(@g2), @g2.STEquals(@g1)

,@g1.ToString(), @g2.ToString()

,CASEWHEN@g1ISNULLTHEN’Nulo’ELSE’No Nulo’END

,CASEWHEN@g2ISNULLTHEN’Nulo’ELSE’No Nulo’END;

GO

Se puede ver que ambas variables son iguales, pero por supuesto que no son nulas. En este caso una figura de cualquier tipo vacía es igual a cualquier otra figura vacía. Por ejemplo un POINT es igual a un CIRCULARSTRING si ambos están vacíos.

1. Curvas Equivalentes 1

Es posible con puntos diferentes generar curvas iguales. Ejemplo:

— Curvas Equivalentes

DECLARE@g1geometry,@g2 geometry;

SET @g1 = ‘CIRCULARSTRING(-5 0, -4 3, 0 5)’;

SET@g2=’CIRCULARSTRING(-5 0, -3 4, 0 5)’;    — Equivalente a la anterior: Igual Inicio y Final

— con un punto intermedio en el mismo Circulo

SELECT@g1.STEquals(@g2), @g2.STEquals(@g1)

,@g1.ToString(), @g2.ToString();

GO

En este caso el punto intermedio del arco de la curva puede variar de (-4 3) a (-3 4) y generar siempre la misma curva.

1. Curvas Equivalentes 2

También se generar curvas iguales si se invierte el punto de inicio y el final

— Curvas Equivalentes 2

DECLARE@g1geometry,@g2 geometry;

SET@g1=’CIRCULARSTRING(-5 0, 5 0, 0 -5)’;

SET@g2=’CIRCULARSTRING(0 -5, 5 0, -5 0)’;     — Equivalente, pero punto de inicio y final son estan invertidos

SELECT@g1.STEquals(@g2), @g2.STEquals(@g1)

,@g1.ToString(), @g2.ToString();

GO

1. Curvas que no son Curvas

Algunas secuencias de puntos pueden no generar curvas en el sentido estricto sino más bien generan líneas rectas.

— Curvas que no son curvas

DECLARE@g1geometry=’CIRCULARSTRING(-5 0, -5 0, 0 5)’;    — El punto medio es igual al inicial o al final

DECLARE@g2geometry=’CIRCULARSTRING(-5 0, -3 2, 0 5)’;    — Puntos co-lineares.

DECLARE@g3geometry=’LINESTRING (-5 0, 0 5)’;

SELECT@g1.STEquals(@g3), @g3.STEquals(@g1)

,@g1.ToString(), @g3.ToString()

,@g1.CurveToLineWithTolerance(0.01,0);

SELECT@g2.STEquals(@g3), @g3.STEquals(@g2)

,@g2.ToString(), @g3.ToString()

,@g2.CurveToLineWithTolerance(0.01,0);

En el código se aprecia que un CIRCULARSTRING puede ser igual a un LINESTRING porque el punto medio es en realidad igual al inicial o al final; o porque los puntos están en la misma línea recta.