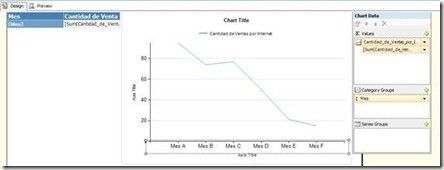
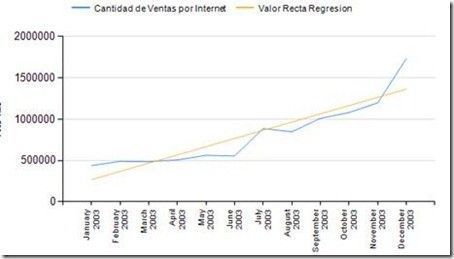
En muchos escenarios nos puede resultar útil poder predecir valores, por ejemplo la cantidad de ventas estimadas para el próximo año de un determinado producto. Hay muchos factores que pueden determinar esa estimación y la mejor forma de dar esa respuesta es el análisis de todas las variables posibles y crear un modelo de minería de datos. Pero, ¿y si la predicción que queremos realizar sobre una serie de valores sólo depende de otra variable? Digamos las ventas de un producto analizadas a través del tiempo. ¿Podemos obtener una estimación para el año que viene? Si, y sin crear modelos de minería… tan sencillo como aplicar Regresión Lineal SimpleEn esta entrada vamos a ver un ejemplo en el que crearemos una medida calculada en MDX que nos devuelva los valores de la recta de regresión. También veremos cómo implementar el cálculo en un informe de Reporting Services para representar esta recta. Les resultará interesante 😉
Refrescando conceptos…
La función de regresión lineal simple es un método estadístico para detectar relaciones entre dos variables, X e Y. A X se le denomina variable independiente que se caracteriza por tener valores fijos y ordenados, medidos sin error. La variable dependiente es Y, sus valores son aleatorios y distribuidos a través del eje de variables dependientes, por encima de la recta X. Y es la variable que queremos predecir. Podemos aplicar la función de regresión lineal cuando sabemos que existe una correlación lineal entre las variable.
La representación de la función es la siguiente:
Y = a + b X + e
Dónde:
a es el valor de la ordenada donde la línea de regresión se intercepta con el eje Y.
b es el coeficiente de regresión poblacional (pendiente de la línea recta)
e es el error
En la práctica se utiliza en múltiples campos, por ejemplo para predecir la cantidad de ventas de un determinado producto. Aquí es dónde ha podido despertar nuestro interés después de un poco de teoría para refrescar nuestra memoria. Es posible implementar este método estadístico para predecir variables o simplemente para hallar una correlación entre una muestra de valores de a ‘explicar’:
“En el estudio de la relación funcional entre dos variables poblacionales, una variable X, llamada independiente, explicativa o de predicción y una variable Y, llamada dependiente o variable respuesta”
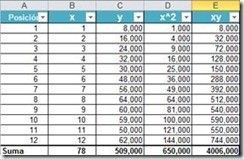
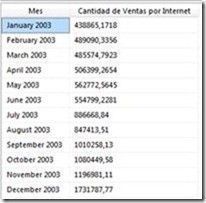
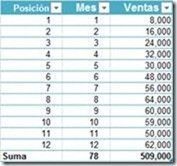
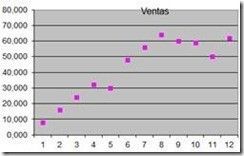
Pongamos un ejemplo. En la siguiente tabla se muestran las ventas obtenidas a través de los distintos meses de un año y su representación gráfica.
 |
 |
Aplicando el método de mínimos cuadrados para resolver la a y b de la función:
| b = (A13*E14-B14*C14)/(A13*D14-(B14*B14))è (12*4006-78*509)/(12*650-(78*78)
b = 4,877622378 |
| a = (C14-C16*B14)/A13è (509-4,877622378*78)/12
a = 11 |
| b | 4,877622378 | Pendiente de la recta |
| a | 11 | Posición respecto al eje |
El valor de b=4,877622378 indica un crecimiento de las ventas en promedio por cada mes que pasa.
El valor de a podría interpretarse como el valor obtenido, en promedio, para el mes Y cuando las ventas son 0.
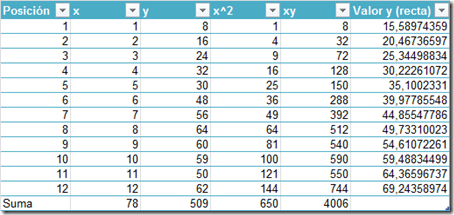
Con estos valores podemos resolver la función que nos devolverá cada punto de la recta:
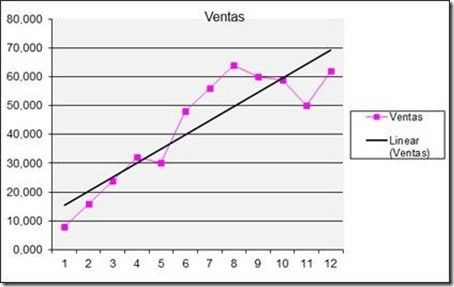
Y con los valores de podemos representar la recta en la gráfica:
Aplicando la teoría
En MDX existen funciones para determinar todos los valores que intervienen en la función de regresión lineal (MSDN):
LinRegIntercept: Calcula la regresión lineal de un conjunto y devuelve el valor de y en la recta de regresión, y = ax + b. El valor de la a en el ejemplo anterior (11).
LinRegPoint: Calcula la regresión lineal de un conjunto y devuelve el valor de y en la recta de regresión, y = ax + b. El valor del punto en la recta.
LinRegSlope: Calcula la regresión lineal de un conjunto y devuelve el valor de la pendiente en la recta de regresión, y = ax + b. El valor de b.
LinRegR2: Calcula la regresión lineal y devuelve el coeficiente de determinación, R2.
LinRegVariance: Devuelve la varianza asociada a la recta de regresión, y = ax + b.
Para nuestro ejemplo vamos a diseñar una consulta con un miembro calculado sobre la base de datos OLAP Adventure Works (versión 2008 r2), que puedes encontrar en codeplex.
Creando la consulta MDX
Como vimos anteriormente, la función que vamos a utilizar para representar la recta de regresión lineal es LinRegPoint, que tiene la siguiente sintaxis:
| LinRegPoint(Slice_Expression_x, Set_Expression, Numeric_Expression_y [ ,Numeric_Expression_x ] ) |
En el ejemplo con el que apoyamos la teoría, el argumento Slice_expression los sustituiremos por el ordinal de meses. El argumento Set_Expression será el conjunto de valores X, los meses en nuestro caso. Numeric_expression es el conjunto de valores para la Y. Finalmente Numeric_Expression tendrá el mismo valor que el primer argumento Slice_expression, el valor posicional del mes.
Vamos paso por paso. En primer lugar vamos a crear un conjunto con el rango de meses con el que vamos a trabajar:
| SET [Meses_2003] as(
[Date].[Calendar].[Month].&[2003]&[1]:[Date].[Calendar].[Month].&[2003]&[12] ) |
Como puedes ver, he elegido los meses del año 2003 que es el último completo en el cubo Adventure Works.
En segundo lugar creamos un miembro calculado para obtener el ordinal de cada mes con respecto a su posición en la dimensión, utilizamos la función RANK()
| MEMBER [Measures].[RankMeses] asRank([Date].[Calendar].currentmember,
[Date].[Calendar].currentmember.level.members) |
Con estas dos expresiones MDX tenemos cubiertos 3 de 4 argumentos de la función LinRegPoint. Ahora vamos a definir el cálculo que nos devuelve el valor del punto que formará la recta de regresión:
| MEMBER [Measures].[Valor Recta Regresion] AS LinRegPoint
( [Measures].[RankMeses] //ordinal por mes , [Meses_2003] //conjunto de meses (X) , [Measures].[Internet Sales Amount] //muestra de valores para el conjunto (Y) , [Measures].[RankMeses] ) |
Y escribimos la consulta completa para ver los resultados:
| WITHSET [Meses_2003] as
( [Date].[Calendar].[Month].&[2003]&[1]:[Date].[Calendar].[Month].&[2003]&[12] ) MEMBER [Measures].[RankMeses] as Rank([Date].[Calendar].currentmember, [Date].[Calendar].currentmember.level.members)
MEMBER [Measures].[Valor Recta Regresion] AS LinRegPoint ( [Measures].[RankMeses] //ordinal por mes , [Meses_2003] //conjunto de meses (X) , [Measures].[Internet Sales Amount] //muestra de valores para el conjunto (Y) , [Measures].[RankMeses] ) |
| SELECT {[Measures].[Internet Sales Amount], [Measures].[RankMeses]
, [Measures].[Valor Recta Regresion]} ON 0, [Meses_2003] ON 1 FROM [Adventure works] |
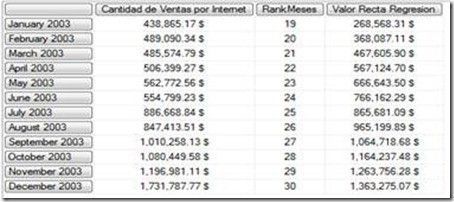
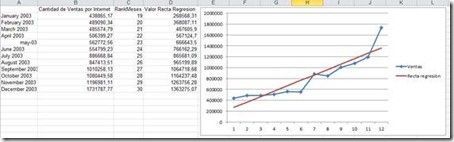
Que muestra los siguientes datos:
La forma más sencilla de visualizar la gráfica que se dibuja con estos valores es llevarlos a Excel:
Además esto nos permite comprobar si efectivamente la recta de regresión se encuentra correctamente calculada. En Excel disponemos automáticamente del cálculo de la función de regresión lineal utilizando las ‘líneas de tendencia’ (BOL).
Depende de la versión de Excel que utilices, te en cuenta este KB211967 Fórmula de la línea de tendencia de gráfico es inexacto en Excel
Seleccionando la línea de valores de ventas pulsa haz clic con el botón derecho y selecciona Línea de Tendencia (o Trendline)
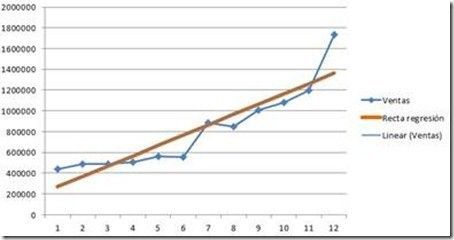
Y se observa cómo se dibuja exactamente sobre la que nos ha devuelto la consulta MDX. Para facilitar la visualización puedes cambiar el grosor de la recta de regresión:
Guay, no? Pero… ¿Para qué queremos crear un cálculo en MDX si Excel ya nos lo hace de forma automática? Para implementarlo en informes de Reporting Services
Implementando en Reporting Services
La única peculiaridad que tiene esta implementación es que se vuelve necesario deshacerse del asistente para consultas MDX, el Query Designer, y pasar la consulta a modo manual MDX para poder utilizar los parámetros del informe (Obligatorio para SQL2005).
Vamos a generar un informe sencillo, conectado al cubo Adventure Works 2008, en el que aparezcan las ventas por internet, segmentadas por los meses del año 2003. De forma complementaria vamos a añadir los cálculos escritos en el bloque anterior: RankMeses y ValorRectaLineal.
Paso 1: Consulta básica – Query Designer
Creamos un informe en un proyecto de Reporting Services en BIDS, añadiendo el origen de datos que apunte al cubo Adventure Works 2008.
En el Query Designer, añadimos la medida Cantidad de Ventas por Internet y el atributo mes de la jerarquía Calendario de la dimensión Fecha:
En el panel superior, configuramos un filtro de rango inclusivo y seleccionamos el mes de Enero de 2003 como primer parámetro y Diciembre de 2003 como último, marcando las casillas de que queremos convertirlos en parámetros del informe.
Pulsa Ok para generar el dataset principal. También se crearán los parámetros de informe y sus respectivos datasets.
Cuando finaliza el asistente nos sitúa en la pestaña de diseño, en la que haremos algunos retoques para añadir un gráfico de líneas con el campo meses como categoría y el campo Cantidad de ventas por Internet como valores:
Con esto hemos generado el “esqueleto” de nuestro informe.
Paso 2: Consulta MDX
Volvamos a editar nuestro dataset. Añadimos el miembro calculado RankMeses que habíamos escrito anteriormente
 |
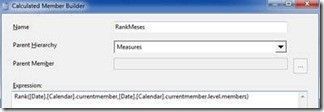
MEMBER [Measures].[RankMeses] as Rank([Date].[Calendar].currentmember, [Date].[Calendar].currentmember.level.members) |
Añade el miembro calculado a la región de datos para que forme parte del Select de la consulta.
Ahora es cuando nos toca tocar la consulta MDX para adaptarla a nuestras necesidades. Para ello pulsamos el botón con el tooltip “Modo diseño”
Hay que observar como el asistente ha implementado los parámetros de fecha desde/hasta en la consulta (Si, el Query Designer no formatea el MDX… ):
| SELECT NON EMPTY { [Measures].[RankMeses], [Measures].[Internet Sales Amount] } ON COLUMNS, NON EMPTY { ([Date].[Calendar].[Month].ALLMEMBERS ) } DIMENSION PROPERTIES MEMBER_CAPTION, MEMBER_UNIQUE_NAME ON ROWS FROM ( SELECT ( STRTOMEMBER(@FromDateCalendar, CONSTRAINED) : STRTOMEMBER(@ToDateCalendar, CONSTRAINED) ) ON COLUMNS FROM [Adventure Works]) CELL PROPERTIES VALUE, BACK_COLOR, FORE_COLOR, FORMATTED_VALUE, FORMAT_STRING, FONT_NAME, FONT_SIZE, FONT_FLAGS |
Este es el rango que debemos añadir a nuestro cálculo de la recta de regresión para que cuando el usuario cambie el rango de fechas a visualizar en el informe, el valor se adapte correctamente. En resumen, hay que añadir la expresión escrita anteriormente cambiando el set [Meses_2003] por el rango de fecha compuesto por los parámetros desde/hasta:
| MEMBER [Measures].[ValorRectaRegresion] as LinRegPoint(
[Measures].[RankMeses], ( STRTOMEMBER(@FromDateCalendar, CONSTRAINED) : STRTOMEMBER(@ToDateCalendar, CONSTRAINED) ) , [Measures].[Internet Sales Amount], [Measures].[RankMeses] ) |
Falta añadir la nueva medida calculada a la consulta, finalmente la consulta MDX debe tener este aspecto:
| WITH MEMBER [Measures].[RankMeses] AS Rank([Date].[Calendar].currentmember, [Date].[Calendar].currentmember.level.members) MEMBER [Measures].[ValorRectaRegresion] as LinRegPoint ( [Measures].[RankMeses], ( STRTOMEMBER(@FromDateCalendar, CONSTRAINED) : STRTOMEMBER(@ToDateCalendar, CONSTRAINED) ) , [Measures].[Internet Sales Amount], [Measures].[RankMeses]) SELECT NON EMPTY { [Measures].[RankMeses], [Measures].[Internet Sales Amount], [Measures].[ValorRectaRegresion] } ON COLUMNS,NON EMPTY { ([Date].[Calendar].[Month].ALLMEMBERS ) } DIMENSION PROPERTIES MEMBER_CAPTION, MEMBER_UNIQUE_NAME ON ROWS FROM ( SELECT ( STRTOMEMBER(@FromDateCalendar, CONSTRAINED) : STRTOMEMBER(@ToDateCalendar, CONSTRAINED) ) ON COLUMNS FROM [Adventure Works]) CELL PROPERTIES VALUE, BACK_COLOR, FORE_COLOR, FORMATTED_VALUE, FORMAT_STRING, FONT_NAME, FONT_SIZE, FONT_FLAGS |
Completo. Ya tenemos implementado en un informe de Reporting Services el cálculo, solo resta añadir el valor a la gráfica:
Tip: Ten en cuenta que es necesario ordenar los meses!
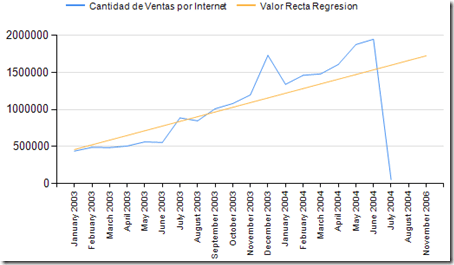
Si en el rango de fecha seleccionamos un mes futuro en el que no existan valores de ventas, la recta representará la predicción de ventas para ese periodo.
Espero que les sea útil 🙂
Enlaces de interés
Teoría de Regresión Lineal (español):
· http://es.wikipedia.org/wiki/Regresi%C3%B3n_lineal
· http://www.uoc.edu/in3/emath/docs/RegresionLineal.pdf
MDX (inglés):
· http://www.mosha.com/msolap/articles/mdxlinreg.htm
· http://cwebbbi.wordpress.com/2007/05/19/using-linear-regression-to-calculate-growth/
· http://www.sqlservian.com/2010/09/mdx-and-linear-regression-an-example/