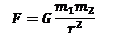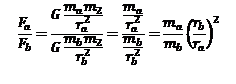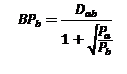Desde hace poco menos de unos 6 meses estoy trabajando con un modelo que permite predecir o estimar las ventas de una tienda, agencia o centro comercial (Mall). Este proyecto es una prueba de concepto que de SQL 2008, realizamos en México, para una empresa financiera: Nacional Monte de Piedad. Quiero escribir de algunos resultados de este ejercicio, pero me pareció apropiado poner algo de contexto académico previo, y esta entrada va en este sentido.
A continuación siguen los fundamentos teóricos e historia de los modelos de teorías gravitacionales, pero antes es interesante entender el problema que resuelve. Piense porque en un centro comercial (Mall), los restaurantes del “Food Court” venden grandes volúmenes cada uno y que locales del mismo tamaño fuera del “Food Court” venderían muchísimo menos; ¿porque en casi todas las ciudades hay una calle que tiene una gran cantidad de casas de empeño muy cercanas una de la otra?, ¿no venderían mas si no estuvieran justo a la par de la competencia?; o ¿porque las zapaterías pequeñas con frecuencia venden más cuando están unas junto a otras?. La respuesta es la ley gravitación J
Los modelos de predicción de ventas al detalle se inician con la “Ley gravitacional del comercio al Detalle de Reilly” que estima el área de influencia de diferentes ciudades. La hipótesis original del modelo es que las ciudades tienen un comportamiento equivalente a la ley de la gravedad. Si abrimos los viejos libros del colegio, podemos recordar que la ley gravitacional universal de de Newton dice:
La fuerza de la gravedad es la fuerza que de atracción que mutuamente ejercen entre sí dos objetos y es directamente proporcional al producto de las masas e inversamente proporcional al cuadrado de la distancia que las separa. Llamamos G a una constante gravitatoria universal que es igual a 6.67 x 10-11Nm2/Kg2.
Aplicando este tipo de pensamiento al área de influencia (o sea al área que realiza sus compras en una ciudad determinada), William Reilly, estableció que partiendo de la formula de la fuerza de gravedad, podemos calcular la relación que tiene la fuerza de atracción de 2 ciudades (A y B) respecto a una población ubicada cerca de ellas. Iniciando con la ley de la fuerza de la gravedad y simplificando, esta puede expresarse como:
Esto puede interpretarse como que la relación entre la atracción de una ciudad A y una ciudad B sobre una población puede expresarse como directamente proporcional a la relación sus masas e inversamente proporcional al cuadrado de la relación de las distancias que separan a la población de las ciudades. Numéricamente hablando, si vivo a 20 Km de una ciudad de 300,000 habitantes (Ciudad A) y a 5 Km de una ciudad de 40,000 habitantes (Ciudad B), entonces la relación es: 0.4687. O sea por cada dólar que gastó en la ciudad B, gastaré 46 centavos en la ciudad A. Un elemento interesante a evaluar es el impacto que la distancia que es más que proporcional. O sea si la ciudad B está a 10 Km, en lugar de 5 Km, la relación cambia a: 1.875, que debe interpretarse como que por cada dólar que gasto en la ciudad B, gastaré dólar ochenta y siete en la ciudad A, un cambio más que proporcional.
Sobre este modelo, se elaboro uno adicional (Curtis), que en lugar de buscar la proporción asume que la decisión es “absoluta”. Compró en una ciudad o en otra, por lo que debemos buscar la distancia que logre que la relación sea 1, que es el punto de “equilibrio”. Debe interpretarse que para distancias más cercanas voy siempre a la ciudad B, para distancias más lejanas siempre ira a A. La fórmula del punto de equilibro para la ciudad B es:
En nuestro caso si las dos ciudades de (300,000 y 40,000 habitantes respectivamente) están a 25 km (20 +5) una de otra el punto de equilibrio seria: 6.687 Km, que debe interpretarse como si vivo a menos de esta distancia de B, compro en B, sino vivo más largo compró en A. Más adelante seguiremos con el Modelo de Huff…